Kurs układania kostki 2x2x2 metodą Guimond

Wprowadzenie

Metoda ta została opracowana przez Gaetan'a Guimond'a. Jest to jedna z ciekawszych a zarazem najszybszych metod układania kostki 2x2x2.

Kolejne kroki układania:

• Trzy narożniki - układamy 3/4 jednej ścianki traktując kolory tak jak napisane powyżej.
• Układamy drugą ściankę - nadal traktując np. biały/żółty jako jeden.
• Zamiana narożników - sprowadzamy odpowidnie kolory do swoich ścianek.
• Permutacja - permutujemy obydwie warstwy - to samo co w Ortedze.

Trzy narożniki

Pierwszym etapem podczas układania jest sprowadzenie trzech narożników w przeciwnych kolorach do jednej ścianki. W 90% procentach przypadków ten etap jest już wykonany a jeżeli nie to nie powinien zająć więcej niż 1-2 ruchy.

Aby przejść do następnego etapu musimy tutaj rozróżnić dwa przypadki. Kolor fioletowy widoczny na ilustracjach to dowolna para kolorów ze ścianek leżących naprzeciwko siebie (w większości przypadków będzie to: biały/żółty, zielony/niebieski, czerwony/pomarańczowy):

Przykładowe wyglądy kostek:

Dwie ścianki

Drugim etapem podczas układania będzie ułożenie dwóch ścianek (tak jakby). Do wyboru mamy dwa początkowe przypadki.

Gdy otrzymamy przypadek 1

Wykonujemy ruch x2 (obracamy kostką - obecna górna ścianka - nasz przypadek 1 - ma się znaleźć na dolnej ściance). Teraz nie kręcąc dolną ścianką, rozpoznajemy górną ściankę i obracamy (używając ruchów U, U', U2) aby otrzymać któryś z przypadków poniżej. Jak poprzenio, kolor fioletowy to dowolna kombinacja przeciwległych kolorów na kostce (przeważnie są to biały/żółty, niebieski/zielony, pomarańczowy/czerwony):

Ilustracja	Algorytm
	(y2) R U' R'
	(y') R' F' R
	(yF' L2 F
	L2' U L'
	(x2) R U' B L'
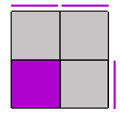	R2 F2 U F
	F' R U' F2 U'
	R F2 U' R2 F U'

Gdy otrzymamy przypadek 2

Wykonujemy ruch x2 (obracamy kostką - obecna górna ścianka - nasz przypadek 2 - ma się znaleźć na dolnej ściance). Teraz nie kręcąc dolną ścianką, rozpoznajemy górną ściankę i obracamy (używając ruchów U, U', U2) aby otrzymać któryś z przypadków poniżej. Jak poprzenio, kolor fioletowy to dowolna kombinacja przeciwnych kolorów (biały/żółty, niebieski/zielony, pomarańczowy/czerwony):

Ilustracja	Algorytm
	(y) R' U R
	L U L'
	(y2) R U2 R'
	(y) L2 D' R
	R U' B L'
	F2 R2 U' R'
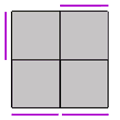	R' F U' F2 U
	x U R' U' R U2 R

Zamiana narożników

Wynikiem poprzednich etapów jest to, że na dwóch ściankach mamy dowolnie rozmieszczone narożniki o kolorach z naprzeciwległych ścianek kostki.

Naszym zadaniem w tym etapie jest taka zamiana miejscami narożników aby dwie ścianki leżące naprzeciwko siebie miały ułożony kolor.

Jest to bardzo proste do wykonania bez użycia/nauki algorytmów ale na wszelki wypadek podaję je ponieżej.

Ilustracja (góra - dół)	Algorytm
	R2U2F2
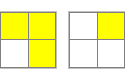	R2U'R2
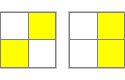	R2U'R2U'R2

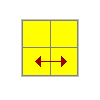
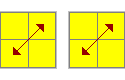
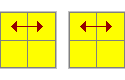
Permutacja warstw

Ostatnim etapem jest permutacja obu warstw (jeżeli znasz już metodę Ortega to z pewnością zauważysz, że są to te same algorytmy).

Ilustracja (góra - dół)	Ilustracja - ogólny podgląd kostki	Algorytm
		(R'F)(R'F2RU'R'F2R2)
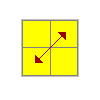		RU'R'U'F2U'RUR'DR2
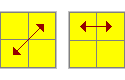		LD'LF2L'DL'
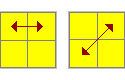		RU'RF2R'UR'
		R2F2R2
		R2UR2'(U2y')R2UR2' - lub zamiast (U2y') można (UD)