Kurs układania kostki 3x3x3 metodą Fridrich

Metoda Fridrich jest najpopularniejszym sposobem układania standardowej kostki 3x3x3. Jest ona rozwinięciem metody LBL poprzez połączenie kilku etapów w jeden. Pozwala znacznie zredukować osiągany czas ale powoduje, że musimy zapoznać się z 78. algorytmami (OLL - 57, PLL - 21).

Wprowadzenie

Tak prezentuje się podział etapów układania:

• Krzyż (tzw. cross) - ułożenie krawędzi pierwszej warstwy tak aby były zgodne ze środkami ścianek bocznych.
• F2L (first two layers) - wstawianie rogów i odpowiadających im krawędzi jednocześnie do odpowiedniego "slotu".
• OLL - orientowanie rogów i krawędzi ostatniej warstwy tak aby otrzymać cały kolor. Tutaj już niestety zaczynają się schody. Na pierwszy rzut oka, gdy zwykły śmiertelnik widzi 57 algorytmów do nauczenia to niemalże mdleje. Specjalnie dla takich osób powstało uproszczenie, które ma na celu rozbicie OLL na 2 etapy przez co ilość algorytmów spada do 10! Odrazu lepiej? Jednak z tą zmianą wiążą się także słabsze czasy.
• PLL - permutacja rogów i krawędzi ostatniej warstwy czyli inaczej zamiana miejscami odpowiednich klocków aby otrzymać gotową kostkę! 21 algów można uprościć do 2 (choć jeżeli już upraszczać to najlepiej do około 6-7) ale z dosyć sporą stratą czasową.

Uproszczenie:

• EO - orientacja krawędzi. Najpierw orientujemy krawędzie. Możliwych przypadków jest 3.
• CO - orientacja rogów. W nagrodę otrzymujemy cały kolor! Algorytmów mamy 7.
• PLL - uproszczona wersja pll'a. Tylko 2 algorytmy ale niestety wymagające powtórzenia.

Kolejność nauki

Nauka algorytymów w odpowiedniej kolejności pozwoli cieszyć się z układania kostki a zarazem systematycznie osiągać lepsze czasy. Sugerowana przeze mnie kolejność jest następująca:

• Krzyż
• F2L (intuicyjnie)
• Uproszczony OLL (EO, CO)
• Uproszczony PLL
• Pełny PLL
• Pełny OLL
• F2L (algorytmy)

Zalecam naukę pełnego PLLa przed nauką pełnego OLLa. Algorytmy do uproszczonego OLLa (EO i CO) są stosunkowo szybkie przez co nauka pozostałych na początku nie da dużego obniżenia czasów układania.

Krzyż (cross)

Może się wydawać, że ułożenie krzyża jest banalnie proste ale nie do końca. Sam fakt ułożenia 4 krawędzi jest trywialny o tyle zaplanowanie a następnie faktyczne ułożenie w jak najmniejszej ilości ruchów i czasie już takie proste nie jest. Jedynym sposobem jest po prostu trening. Warto pamiętać, że większość przypadków można rozwiąząć w około 6 ruchach.

Dwie pierwsze warstwy (F2L - First Two Layers)

F2L jest to etap polegający na jednoczesnym wstawianiu odpowiedniego narożnika i krawędzi w przeznaczone im miejsce. Dzieki temu otrzymujemy od razu gotowe dwie warstwy.

Mimo dużej ilości przypadków, opanowanie tego etapu w stopniu zadowalającym nie jest trudne. Większość jest stosunkowo łatwa w rozwiązaniu i dlatego można zastosować jedną z dwóch metod nauki:

• wymyślenie własnych algorytmów (intuicyjnie)
• skorzystanie z gotowych algorytmów

Na początek polecam próbę samodzielnego układania bez korzystania z gotowych algorytmów. Na pewno nic na tym nie stracicie a można zyskać dużą przyjemność i satysfakcję z ułożonej kostki.

Uproszczony OLL

EO

Pierwsza cześć z uproszczonego OLLa polega na ułożeniu krawędzi górnej warstwy. Krawędzie utworzą krzyż podobny do tego jak w pierwszym etapie układania na dolnej ściance.

Ilustracja	Algorytm
	F (R U R' U') F'
	F (U R U' R') F'
	(R U2) (R2 F R F') U2 (R' F R F')

CO

W drugiej część ułożymy narożniki tak aby na górnej ściance otrzymać kolor.

Ilustracja	Algorytm
	(y2) z' (U' R U R' U' R U) L' (U' R' U R U' R' U) (R2 D') (R U2 R' D) (R U2 R) (y2) (R2 D) (R' U2) (R D') (R' U2 R')
	R' U' R U' R' U R U' R' U2 R (y') R U2 R' U' R U R' U' R U' R' (y) F (R U R' U') (R U R' U') (R U R' U') F'
	R U2 R2 U' R2 U' R2 U2 R (R' U) (L U') (R U') (L' U' L U' L')
	r' U' R U L U' R' U F R F' r U R' U' r'
	R U R' U R U2 R' y L' U2 L U L' U L
	L' U' L U' L' U2 L (y') R U2 R' U' R U' R'
	(x') D (R U R' D') (R U' R') (y2) x U R' U' L U R U' r' (y') F' r U R' U' r' F R R' F' L' F R F' L F R' U' (R U R' F') (R U R' U') (R' F R2)

Uproszczony PLL

Uproszczenie PLL to nic innego jak po prostu wyłuskanie spośród 21 algorytmów tych, które pozwolą nam wykonać wszystkie przypadki. Najbardziej skrajne uproszczenie składa się z 2 (+2 lutrzane odbicia) algorytmów. Mamy bardzo dużą stratę czasową ponieważ w niektórych sytuacjach musimy powtarzać jeden algorytm nawet do trzech razy!

Ilustracja	Oznaczenie	Algorytm(y)
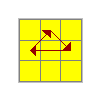	U	(R' U R' U') (R' U' R' U) (R U R2) (y2) M' U2 M U' M' U2 M U' M' U2 M (y2) L' U L' U' L' U' L' U L U L2
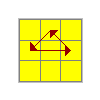	U	(L U' L U) (L U L U') (L' U' L2) (y2) M' U2 M U M' U2 M U M' U2 M (y2) R U' R U R U R U' R' U' R2 (y2) M2 U M U2 M' U M2
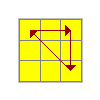	A	R' F R' B2 R F' R' B2 R2 (x) R' U R' D2 R U' R' D2 R2
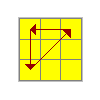	A	L F' L B2 L' F L B2 L2 (y x) R2 D2 R U R' D2 R U' R

Pełny OLL

Po tym etapie otrzymamy kolor na górnej ściance kostki. Mamy tutaj 57 algorytmów do nauki. Bez obaw, nie musisz od razu opanowywać wszystkich. Najlepiej zacząć od tych z uproszczenia a następnie na spokojnie dokładać kolejne.

Ilustracja	Algorytm(y)
	x' (r R' U') y' (R' U) (R U R U R' d') (r' R) M U R U R' U' M2 U R U' r' r' (R U) (R U R' U' r2) (R2' U) (R U') r'
	(R U2) (R2 F R F') U2(R' F R F') (R U) B' (l U l' R' U') (R' F R F') R U2 R2 y' x' (R U R') x y U2 R' y (L' F L')
	x (R' U R U') B2(R' U R U2) y (R2 U) (y) F (R U R' U') S (R U R' U') f'
	(R r' U' r U2 r' U') (R U' R2) L
	(L' l U l' U2 l U) (L' U L2) R'
	(R' F R F') U' (r R') y' (R' U l Us) y2 R U R' U R' F R F' U2 R' F R F'
	(R U2) B' (R' U' R U) y (R2 U2 R' F')
	F (R U R' U) y' (R' U2) (R' F R F')
	(R' U2) (R2 U) (R' U R U2) x' (U' R' U)
	x (r' R U R' U' r) (R' U R U') (R U R' U') (M U R U') r' M' U' M U M' U' M U' M' U2 M
	F (R U R' U' R) y' (R' F R B' R' F')
	(R' U' R U' R' d) (R' U l U)
	F (U R U' R' U R U' R') F' (y2) f (R U R' U') (R U R' U') f'
	x' (R U' R' F' R U R') x y (R' U R) y2 F U R U2 R' U' R U R' F'
	x' (L' U L F L' U' L) x y' (L U' L') y2 F' U' L' U2 L U L' U' L F
	(r' U' r) (R' U' R U) (r' U r)
	(l U l') (L U L' U') (l U l')
	F (R U R' U') F'
	R U R' U' R' F R F' R U R' F2 L F L' U' F
	(R' U' R U) x' D (R U' R' Us) (y2) R U R2 U' R' F R U R U' F'
	(R' F R U R' d') L' d R R' F R U R' U' F' U R
	(L F' L' U' L d) R d' L' L F' L' U' L U F U' L'
	(R U) x' (R U' R' U) x (U' R') R' U' R' F R F' U R
	R' (L F' L') (R U2 R') (L F' L') R (y') M' U M U2 M' U M (y) r U R' U' r' R U R U' R'
	l U L' U L U' L' U L U2 l'
	r' U' R U' R' U R U' R' U2 r
	x' (L' U L') (U' L2) b' F' (L' U L U')
	x' U' (R U2) (l' U2) (R' U2 l U')
	F (R U R' U' R U R' U') F'
	F' (L' U' L U L' U' L U) F
	(r' U') (R U' R' U2 r)
	(l U) (L' U L U2 l')
	F (R U R' U') F' y F (R U R' U') F'
	F' (L' U' L U) F y' F' (L' U' L U) F
	(R U R') y x (R' U l U' l' U' R)
	(L' U' L) y' x (L U' r' U r U L')
	(L' U' L) y' x (L U' r' U r U L') U F R' F' R U R U' R' y F R U' R' U' R U R' F y R' F R F' U' F' U F
	(R U2) (R2 F R F' R U2 R')
	(r' U2) (R U R' U r)
	(l U2) (L' U' L U' l')
	(F R') (F R2 U' R' U' R U R' F2)
	(F' L) (F' L2 U L U L' U' L F2)
	(R' U) (R U2 R' d') (L' U L d R)
	(L U') (L' U2 L d) (R U' R' d' L')
	(R d) (L U' r' U') (y) F U R U' R' F'
	(L' d') (R' U l U) (y') F' U' L' U L F
	(R d) (L' d') (R' U l U l')
	(L' d') (R d) (L U' r' U' r)
	(y2) L' U' L U' L' U L U' L F' L' F (R' U' R U' R' U R) U x' (R U' R' U)
	(y2) R U R' U R U' R' U' R' F R F' (L U L' U L U' L') U' x' (L' U L U')
	(y2) z' (U' R U R' U' R U) L' (U' R' U R U' R' U) (R2 D') (R U2 R' D) (R U2 R) (y2) (R2 D) (R' U2) (R D') (R' U2 R')
	R' U' R U' R' U R U' R' U2 R (y') R U2 R' U' R U R' U' R U' R' (y) F (R U R' U') (R U R' U') (R U R' U') F'
	R U2 R2 U' R2 U' R2 U2 R (R' U) (L U') (R U') (L' U' L U' L')
	r' U' R U L U' R' U F R F' r U R' U' r'
	R U R' U R U2 R' y L' U2 L U L' U L
	L' U' L U' L' U2 L (y') R U2 R' U' R U' R'
	(x') D (R U R' D') (R U' R') (y2) x U R' U' L U R U' r' (y') F' r U R' U' r' F R R' F' L' F R F' L F R' U' (R U R' F') (R U R' U') (R' F R2)

Pełny PLL

Ostatni etap na drodze do ułożonej kostki. Dokonujemy permutacji (przemieszczenia) elementów ostatniej warstwy aby ostateczenie ułożyć kostkę. Mamy 21 algorytmów. Warto zacząć od wersji uproszczonej i tak jak w poprzednim etapie - dokładać kolejne. Warto poznać wszystkie 21 algorytmów PLL zanim zaczniemy naukę wszystkich algorytmów OLL.

Ilustracja	Oznaczenie	Algorytm(y)
	U	(R' U R' U') (R' U' R' U) (R U R2) (y2) M' U2 M U' M' U2 M U' M' U2 M (y2) L' U L' U' L' U' L' U L U L2
	U	(L U' L U) (L U L U') (L' U' L2) (y2) M' U2 M U M' U2 M U M' U2 M (y2) R U' R U R U R U' R' U' R2 (y2) M2 U M U2 M' U M2
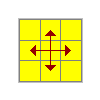	H	M2 U M2 U2 M2 U M2 R2 U2 R2 U2 R2 U R2 U2 R2 U2 R2 U' x2 M2 d M2 d2 M2 d M2
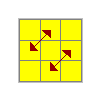	Z	x' (R U' R' U) (D R' D) U' (R' U R) (D2 F) M2 D y M2 D' y' S M2 S' U R' (U' R U' R) (U R U' R') (U R U R2) (U' R' U) U2 M2 U M2 U M' U2 M2 U2 M' R U R' U R' U' R' U R U' R' U' R2 U R U2
	A	R' F R' B2 R F' R' B2 R2 x R' U R' D2 R U' R' D2 R2
	A	L F' L B2 L' F L B2 L2 y x R2 D2 R U R' D2 R U' R
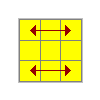	E	x (U R' U' L) (U R U' r2 U' R U) (L U') (R' U) (z) U2(R2 F) (R U R' U' R U R' U' R U R' U') F' (R2 U2) x U R' U' L U R U' L' U R U' L U R' U' L' Fl' U' L U R U' r' F R F' r U R' U' r' F R' F' r U R U' r' F R F' r U R' U' r'
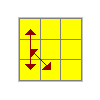	J	B2 R' U' R B2 L' D L' D' L2 y2 R' U2 R U R' U2 L U' R U L' U R' U L' U2 R U' R' U2 R L U R' U L' U2 R U' R' U2 R L U2
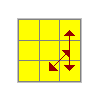	J	B2 L U L' B2 R D' R D R2 U' L U' R U2 L' U L U2 R' L'
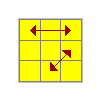	R	(R' U2) (R U2) (R' F R U R' U' R' F' R2)
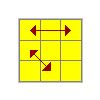	R	(L U2) (L' U2) (L F' L' U' L U L F L2)
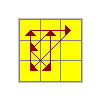	G	(R U R') y' (R2 u' R U') (R' U R' u R2)
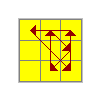	G	(L' U' L) y (L2 u L' U) (L U' Lu' L2)
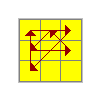	G	(R2 u) (R' U R' U' Ru' R2) y (L' U L)
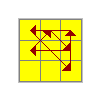	G	(L2 u') (L U' L U L' u L2) y' (R U' R')
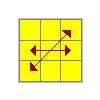	N	(L U') (R U2) (L' U L) (R' U' R) U2 L' U R'
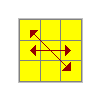	N	(R' U) (L' U2) (R U' R') (L U L') U2 R U' L
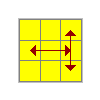	T	(R U R' U' R' F R2 U' R' U') (R U R' F')
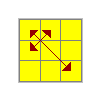	Y	(R2 U' R2 U' R2 U) y' (R U R') B2(R U' R') F R U' R' U' R U R' F' R U R' U' R' F R F'
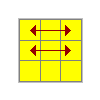	F	(R' U R U' R2) y' (R' U' R U) y x (R U R' U' Rl) R' U R U' R2 F' U' F U R x U R' U' R2
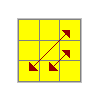	V	L' U R U' L U L' U R' U' L U2 R U2 R' y' R' U R' U' y R' F' R2 U' R' U R' F R F