Kurs układania kostki Square-1

Square-1 jest dość interesującym rodzajem kostki. Wielu niedoświadczonym osobom już samo pomieszanie sprawia problemy. Aby tego uniknąć musimy zrozumieć jak przemieszczają się poszczególne klocki oraz kiedy i jakie ruchy możemy wykonać.

Wprowadzenie i notacja

Przed rozpoczęciem układania ważne jest również zrozumienie zapisu notacji jaki będziemy stosować.

W Square-1 operujemy dwoma warstwami. Górną i dolną, a więc zapis (x,y) oznacza pewien ruch warstwą górną (x) oraz dolną (y). Po każdym z takich nawiasów następuje obrót prawą ścianką o 180 stopni (ruch ten zapisany jest w postaci /). Teraz wystarczy zapamiętać pewien schemat postępowania. Mianowicie, pod x kryje nam się obrót górną warstwą o x*30 stopni (30 stopni - mały klocek - krawędź, 60 stopni - duży klocek - narożnik), a pod y kryje nam się obrót dolną ścianką o y*30 stopni. Jeżeli miara kąta jest dodatnia obracamy zgodnie z ruchem wskazówek zegara, natomiast jeżeli miara ta jest ujemna obracamy w przeciwnym ruchu do wskazówek zegara.

Układanie Square-1 można podzielić na 2 głowne etapy:

• Przywrócenie kształtu sześcianu - nazwa mówi za siebie, musimy przywrócić początkowy kształt(sześcian)
• Permutacja i orientacja, która z kolei dzieli się na:
  • Wstawianie narożników - wstawiamy narożniki do odpowiednich warstw
  • Wstawianie krawędzi - j/w ale krawędzie
  • Permutacja narożników - zamieniamy narożniki miejscami
  • Permutacja krawędzi - j/w ale krawędzie
  • Poprawa środkowej warstwy - ustawiamy odpowiednio środkową warstwę (jeżeli konieczne)

Przywrócenie kształtu

Pierwszym etapem podczas układania square-1 jest przywrócenie go pierwotnego kształtu - sześcianu. Poniżej zaprezentowana jest uproszczona wersja tego etapu.

Najprościej będzie zrobić to dwu-etapowo:

1. Sprowadzenie sześciu narozników do jednej warstwy (powstanie wtedy coś na kształt gwiazdki)
2. Przywrócenie kształtu sześcianu.

Gdy już mamy "gwiazdkę" odszukujemy kształt drugiej warstwy na rysunkach poniżej, ustawiamy go na górnej warstwie i wykonujemy algorytm.

Ilustracja	Algorytm
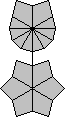	/ (-2,-4) / (-1,-2) / (-3,-3) /
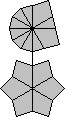	/ (2,-2) / (-3,-4) / (4,-3) / (-5,-4) / (6,-3) /
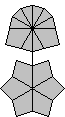	/ (-4,-2) / (-1,4) / (-3,0) /
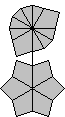	/ (-4,0) / (5,4) / (2,-3) / (-5,-4) / (6,-3) /
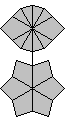	/ (2,2) / (0,-1) / (3,3) /

Wstawianie narożników (orientacja)

Po przywróceniu square'a do porządanego kształtu czas na wstawienie narożników w odpowiednie miejsca.

Poniżej znajdują się możliwe sytuacje i algorytmy do nich. Po lewej to górna ścianka a po prawej dolna.

Ilustracja (góra/dół)	Algorytm
	(1,0) / (-1,0)
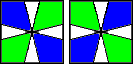	(1,0) / (3,3) / (-1,0)
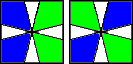	(1,0) / (0,3) / (0,3) / (-1,0)
	(1,0) / (3,0) / (-1,0)

Wstawianie krawędzi (orientacja)

Celem tego etapu jest zakończenie układania koloru zarówno na dolnej jak i na górnej ściance. Poniżej znajdują się sytuacje i algorytmy, za pomocą których osiągniemy nasz cel (po lewej to górna a po prawej dolna ścianka).

Ilustracja (góra/dół)	Algorytm
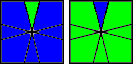	(0,-1) / (-3,0) / (4,1) / (-4,-1) / (3,0) / (0,-1)
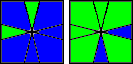	(1,0) / (-3,0) / (-1,-1) / (4,1) / (-1,0)
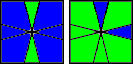	(0,-1) / (3,0) / (-3,0) / (1,-2) / (0,3) / (-1,0)
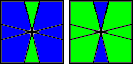	(0,-1) / (1,1) / (-1,0)
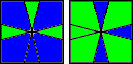	(0,-1) / (1,4) / (-1,-4) / (-3,0) / (4,1) / (-1,0)
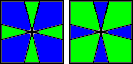	(0,-1) / (1,1) / (3,3) / (-1,-1) / (0,1)

Permutacja narożników

Po uzyskaniu koloru na górnej i dolnej ściance musimy pozamieniać miejscami narożniki.

Poniżej znajdują się sytuacje i algorytmy do nich.

Ilustracja (góra/dół)	Algorytm
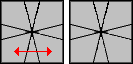	/ (3,-3) / (3,0) / (-3,0) / (0,3) / (-3,0) /
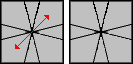	/ (3,3) / (3,0) / (3,3) / (3,0) / (3,3) /
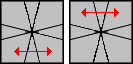	/ (-3,0) / (3,3) / (0,-3) /
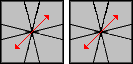	/ (3,-3) / (3,-3) /
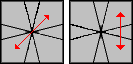	/ (3,0) / (-3,0) / (3,0) / (-3,0) /

Permutacja krawędzi

Powoli zbliżamy się do końca. Przedostatnim krokiem będzie spermutowanie krawędzi.

Poniżej znajdują się sytuacje i algorytmy do nich.

Ilustracja (góra/dół)	Algorytm
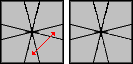	/ (-3,0) / (0,3) / (0,-3) / (0,3) / (2,0) / (0,2) / (-2,0) / (4,0) / (0,-2) / (0,2) / (-1,4) / (0,-3) / (0,3)
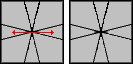	/ (3,3) / (-1,0) / (2,-4) / (4,-2) / (0,-2) / (-4,2) / (1,-5) / (3,0) / (3,3) / (3,0)
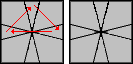	/ (3,0) / (1,0) / (0,-3) / (-1,0) / (-3,0) / (1,0) / (0,3) / (-1,0)
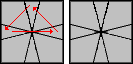	(1,0) / (0,-3) / (-1,0) / (3,0) / (1,0) / (0,3) / (-1,0) / (-3,0) /
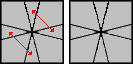	/ (3,3) / (0,3) / (1,1) / (-1,4) / (-3,3) /
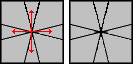	/ (3,-3) / (3,-3) / (0,1) / (-3,3) / (-3,3) / (-1,0)
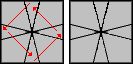	/ (-3,-3) / (0,1) / (-2,2) / (0,2) / (-4,-4) / (-1,0) / (-3,-3) / (0,2) / (-2,-2) / (-1,0)
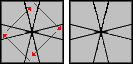	(1,0) / (2,2) / (0,-2) / (3,3) / (1,0) / (4,4) / (0,-2) / (2,2) / (0,-1) / (3,3) /
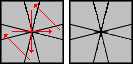	(0,-1) / (1,-2) / (-4,0) / (0,3) / (1,0) / (3,-2) / (-4,0) / (-4,0) / (-2,2) / (-1,0) / (0,3) / (-3,0)
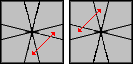	(1,0) / (0,3) / (-1,-1) / (1,-2) / (-1,0)
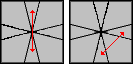	(1,0) / (0,-1) / (0,-3) / (5,0) / (-5,0) / (0,3) / (0,1) / (5,0)
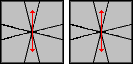	(1,0) / (5,-1) / (-5,1) / (5,0)

Poprawienie środkowej warstwy

Może się zdarzyć tak, że trzeba będzie poprawić środkową warstę po zakończonym układaniu.

Poniżej znajdują się przypadki i algorytmy.

Ilustracja	Algorytm
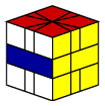	(1,0) / (6,6) / (-1,0)
	/ (6,0) / (6,0) / (6,0)
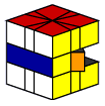	/ (6,0) / (0,6) / (-1,5)